Последовательные игры
До этого мы обсуждали только игры, в которых игроки совершают выбор одновременно. Но есть и другие варианты.
Мало того, такие варианты встречаются достаточно часто.
Рассмотрим следующую игру. Пусть барон Мюнхаузен и Мата Хари собрались на свидание в ресторане, в котором из соображений экономии разделят на двоих одно блюдо. В этой игре функцией полезности каждого игрока будет оценка удовольствия, которое он получил во время этой встречи (как удовольствие от общения с кем-то, так и от выбора ресторана или даже от выбора блюда).
Для того, чтобы никто не обиделся, вначале Мюнхаузен выбирает одно из двух кафе, а потом Мата Хари выбирает одно из двух блюд в нём (блюда в кафе одинаковы, но готовят их по-разному).
Каждая пара исхода принесёт разные выигрыши, выигрышем в данной игре будет полученное удовольствие от поглощения пищи. Так как эти персонажи слишком различны, в своём выборе они руководствуются исключительно эгоистичными соображениями.
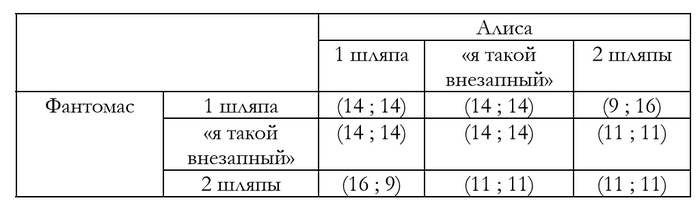
Попробуем описать данную игру в стратегической форме.
Заметим, что когда игра представлена в указанной форме, то мы видим два равновесия по Нэшу (суши в японском кафе или шаурма в кошерном ресторане). На самом деле это не так. Проблема заключается в том, что игроки выбирают стратегии последовательно друг за другом, то есть, второй игрок уже знает, какую стратегию выбрал первый. Матрица платежей в привычной форме не даёт об этом представления.
Асимметричность данной игры лучше проявляется не в виде матрицы платежей, а в виде дерева выбора, экстенсивной форме. Решения в этой форме могут быть представлены этим деревом, каждый узел которого связан с игроком, который принимает решение. Каждый вариант представляет собой ветвь. Выигрыши всех игроков связаны с терминальными вершинами или листьями дерева.
Первым делом барон Мюнхаузен должен выбрать между японскими и кошерными ресторанами, а затем Мата Хари должна выбрать, что она возьмёт — суши или шаурму. Но Мата Хари, делая свой выбор, уже знает, в какой ресторан привёл её барон Мюнхаузен на свидание.
Проведём анализ игры, рассмотрев ходы в обратном порядке. Если Мюнхаузен уже сделал свой первый ход и выбрал японское кафе, то, вне зависимости от хода Мата Хари, выигрыш будет составлять (1 ; 9). Если Мюнхаузен выбрал своим первым ходом кошерный ресторан, то ходы Мата Хари уже неравнозначны и для достижения наилучшего результата ей стоит выбрать шаурму, после чего выигрыш будет составлять (2 ; 1).
Что же выбрать Мюнхгаузену? При выборе японского кафе, результатом игры будет (1 ; 9) и он получит выигрыш, равный 1. Если он выберет кошерный ресторан, то его выигрыш будет равен 2. Это и будет наиболее разумным для него выбором. Это значит, что равновесный выбор — шаурма из кошерного ресторана, что ведёт к выигрышу для Мюнхгаузена в 2 очка, а для Мата Хари – в 1.
Второе из вроде как равновесий, которое было получено с помощью таблицы, точно не является равновесием, имеющим смысл в данной игре. Очевидно, что в случае выбора Мюнхгаузеном японского кафе, Мата Хари могла выбрать суши, но выбор данной столовой Мюнхаузеном был бы не самым умным поступком.
С точки зрения Мата Хари, свидание складывается не самым удачным образом – она могла бы получить выигрыш в 9 очков удовольствия, а получит всего-навсего 1. Что она может сделать в такой ситуации?
Например, она может угрожать Мюнхаузену, что они всё равно будут есть суши, даже если пойдут в кошерный ресторан. Если Мюнхаузен верит в женские угрозы, то это имеет смысл. В таком случае, японское кафе ему принесёт один балл удовольствия, тогда как суши из кошерного ресторана он вообще не захочет есть и получит 0 очков.
Но является ли эта угроза реальной?